Avlod daraxti (guruh nazariyasi) - Descendant tree (group theory)

Matematikada, xususan guruh nazariyasi, a avlod daraxti a ierarxik tuzilish ota-onalar va avlodlar o'rtasidagi munosabatlarni ko'rish uchun izomorfizm sinflari asosiy kuch buyurtmasining cheklangan guruhlari ${ displaystyle p ^ {n}}$, sobit asosiy raqam uchun ${ displaystyle p}$ va o'zgaruvchan tamsayı ko'rsatkichlari ${ displaystyle n geq 0}$.Ushbu guruhlar qisqacha nomlanadi cheklangan p guruhlari.The tepaliklar a avlod daraxti sonli izomorfizm sinflari p-gruplar.

Ularga qo'shimcha ravishda buyurtma ${ displaystyle p ^ {n}}$, cheklangan p-gruplarda yana ikkita bog'liq invariant mavjud, the nilpotensiya sinfi ${ displaystyle c}$ va koklass ${ displaystyle r = n-c}$.Bu ma'lum bir turdagi avlodlar deb ataladigan daraxtlar bo'lib chiqdi kesilgan koklass daraxtlari cheksiz ko'p tepaliklari umumiy koklassga ega ${ displaystyle r}$, takrorlanadigan cheklangan naqshni aniqlang.Bu ikkita hal qiluvchi xususiyat cheklanish va davriylikdaraxtlarning barcha a'zolarining tavsiflarini tan oling, chunki juda ko'p parametrlangan prezentatsiyalar Shunday qilib, avlodlar daraxtlari cheklanganlarni tasniflashda asosiy rol o'ynaydi pyadrolari va maqsadlari vositasida Artin uzatish gomomorfizmlari, avlod daraxtlari qo'shimcha tuzilishga ega bo'lishi mumkin.

Muhim savol - bu nasl daraxtining qanday ekanligi ${ displaystyle { mathcal {T}} (R)}$ aslida qabul qilingan tayinlangan boshlang'ich guruh uchun tuzilishi mumkin ildiz ${ displaystyle R}$ daraxtning p-gruplar yaratish algoritmi - bu ma'lum bir cheklangan avlod daraxtini qurish uchun rekursiv jarayon p- daraxt ildizi rolini o'ynaydigan guruh.Bu algoritm hisoblash algebra tizimlarida amalga oshiriladi GAP va Magma.

Ta'riflar va terminologiya

M. F. Nyumanning so'zlariga ko'ra,^[1]ning bir nechta aniq ta'riflari mavjud ota-ona ${ displaystyle pi (G)}$cheklangan p-grup ${ displaystyle G}$.Umumiy printsip - bu shakllantirishdir miqdor ${ displaystyle pi (G) = G / N}$ ning ${ displaystyle G}$tegishli tomonidan oddiy kichik guruh ${ displaystyle N triangleleft G}$bu ham bo'lishi mumkin

P

1. The markaz ${ displaystyle N = zeta _ {1} (G)}$ ning ${ displaystyle G}$, qayerdan ${ displaystyle pi (G) = G / zeta _ {1} (G)}$ deyiladi markaziy qism ning ${ displaystyle G}$, yoki
2. oxirgi ahamiyatsiz muddat ${ displaystyle N = gamma _ {c} (G)}$ ning pastki markaziy seriyalar ning ${ displaystyle G}$, qayerda ${ displaystyle c}$ ning nilpotentsiya sinfini bildiradi ${ displaystyle G}$, yoki
3. oxirgi ahamiyatsiz muddat ${ displaystyle N = P_ {c-1} (G)}$ ning pastki ko'rsatkichp markaziy seriyalar ning ${ displaystyle G}$, qayerda ${ displaystyle c}$ ko'rsatkichni bildiradi-p sinf ${ displaystyle G}$, yoki
4. oxirgi ahamiyatsiz muddat ${ displaystyle N = G ^ {(d-1)}}$ ning olingan qator ning ${ displaystyle G}$, qayerda ${ displaystyle d}$ ning olingan uzunligini bildiradi ${ displaystyle G}$.

Har holda,${ displaystyle G}$ deyiladi bevosita avlod ning ${ displaystyle pi (G)}$va a yo'naltirilgan chekka daraxt tomonidan belgilanadi ${ displaystyle G to pi (G)}$yo'nalishi bo'yicha kanonik proektsiya ${ displaystyle pi: G dan pi (G)}$ kvitansiyaga ${ displaystyle pi (G) = G / N}$yoki tomonidan ${ displaystyle pi (G) dan G} gacha$ qarama-qarshi yo'nalishda, bu avlod avlodlari uchun odatiy holdir. Oldingi konventsiya C. R. Lidxem-Grin va M. F. Nyuman tomonidan qabul qilingan,^[2]M. du Sautoy va D. Segal tomonidan,^[3]C. R. Lidem-Grin va S. MakKay tomonidan,^[4]va B. Eik, C. R. Lidem-Grin, M. F. Nyuman va E. A. O'Brayen tomonidan.^[5]Oxirgi ta'rif M. F. Nyuman tomonidan qo'llaniladi,^[1]M. F. Nyuman va E. A. O'Brayen tomonidan,^[6]M. du Sautoy tomonidan,^[7]va B. Eik va C. R. Lidem-Grin tomonidan.^[8]

Quyida, barcha qirralar uchun kanonik proektsiyalarning yo'nalishi tanlanadi, keyin umuman, tepalik ${ displaystyle R}$ a avlod tepalikning ${ displaystyle P}$va ${ displaystyle P}$ bu ajdod ning ${ displaystyle R}$, agar bo'lsa ${ displaystyle R}$ ga teng ${ displaystyle P}$yoki bor yo'l

${ displaystyle (1) qquad R = Q_ {0} - Q_ {1} to cdots - Q_ {m-1} - Q_ {m} = P}$, bilan ${ displaystyle m geq 1}$,

dan yo'naltirilgan qirralarning ${ displaystyle R}$ ga ${ displaystyle P}$.Yolni tashkil etuvchi tepaliklar albatta bilan mos keladi takrorlangan ota-onalar ${ displaystyle Q_ {j} = pi ^ {j} (R)}$ ning ${ displaystyle R}$, bilan ${ displaystyle 0 leq j leq m}$:

${ displaystyle (2) qquad R = pi ^ {0} (R) to pi ^ {1} (R) to cdots to pi ^ {m-1} (R) to pi ^ {m} (R) = P}$, bilan ${ displaystyle m geq 1}$,

Ota-onalarning eng ahamiyatsiz bo'lgan (P2) so'nggi muhim bo'lmagan pastki markaziy kvitentsiyalar deb ta'riflangan taqdirda, ularni ketma-ket deb hisoblash mumkin takliflar ${ displaystyle R / gamma _ {c + 1-j} (R)}$ sinf ${ displaystyle c-j}$ ning ${ displaystyle R}$qachon nilpotensiya sinfi ${ displaystyle R}$ tomonidan berilgan ${ displaystyle c geq m}$:

${ displaystyle (3) qquad R simeq R / gamma _ {c + 1} (R) to R / gamma _ {c} (R) to cdots to R / gamma _ {c + 2-m} (R) dan R / gamma _ {c + 1-m} (R) simeq P}$, bilan ${ displaystyle c geq m geq 1}$.

Odatda, avlod daraxti ${ displaystyle { mathcal {T}} (G)}$ tepalikning ${ displaystyle G}$ avlodlarining subtree ${ displaystyle G}$, dan boshlab ildiz ${ displaystyle G}$Mumkin bo'lgan maksimal avlod ${ displaystyle { mathcal {T}} (1)}$ ahamiyatsiz guruh ${ displaystyle 1}$ barcha cheklanganlarni o'z ichiga oladi pguruhlar va biroz istisno, chunki har qanday ota-ona ta'rifi (P1-P4) uchun ahamiyatsiz guruh ${ displaystyle 1}$ cheksiz ko'p abeliyaga ega pOta-ona ta'riflari (P2-P3) har qanday ahamiyatsiz bo'lmagan sonli bo'lishidan afzalliklarga ega p-grup (buyurtma tomonidan bo'linadi ${ displaystyle p}$) faqat juda ko'p yaqin avlodlarga ega.

Pro-p guruhlar va koklass daraxtlari

To'g'ri tushunish uchun koklass daraxtlari avlodlarning ma'lum bir misoli sifatida cheksizga oid ba'zi faktlarni umumlashtirish kerak topologik prop guruhlar.A'zolar ${ displaystyle gamma _ {j} (S)}$, bilan ${ displaystyle j geq 1}$, pro-ning pastki markaziy seriyasidanp guruh ${ displaystyle S}$cheklangan indeksning yopiq (va ochiq) kichik guruhlari va shuning uchun tegishli kotentsiyalar ${ displaystyle S / gamma _ {j} (S)}$ cheklangan p- guruhlar.p guruh ${ displaystyle S}$ deb aytilgan koklass ${ displaystyle mathrm {cc} (S) = r}$qachon chegarasi ${ displaystyle r = lim _ {j to infty} , mathrm {cc} (S / gamma _ {j} (S))}$ ketma-ket kotirovkalarning koklassi mavjud va cheklangan. cheksiz prop guruh ${ displaystyle S}$ koklass ${ displaystyle r}$ a p-adikadan oldingikosmik guruh,^[5]chunki u oddiy kichik guruhga ega ${ displaystyle T}$, tarjima guruhi, bu uzuk ustidagi bepul modul ${ displaystyle mathbb {Z} _ {p}}$ ning pning oddiy sonlari noyob tarzda aniqlangan daraja ${ displaystyle d}$, o'lchov, shunday qilib, bu miqdor ${ displaystyle P = S / T}$ cheklangan p-grup, the nuqta guruhiharakat qiladigan ${ displaystyle T}$ uniserially.O'lchov tomonidan berilgan

${ displaystyle (4) qquad d = (p-1) p ^ {s}}$, ba'zilari bilan ${ displaystyle 0 leq s$.

Markaziy cheklanish cheksiz pro uchun natijap koklass guruhlari ${ displaystyle r}$ deb nomlangan tomonidan taqdim etiladi Teorema D., bu beshtadan biri Coclass teoremalari 1994 yilda A. Shalev tomonidan mustaqil ravishda isbotlangan^[9]va C. R. Lidem-Grin tomonidan,^[10]va 1980 yilda C. R. Lidem-Grin va M. F. Nyuman tomonidan taxmin qilingan.^[2]Teorema D cheksiz pro-ning izomorfizm sinflari juda ko'p, deb ta'kidlaydi.p koklass guruhlari ${ displaystyle r}$, har qanday sobit bosh uchun ${ displaystyle p}$ va har qanday sobit manfiy bo'lmagan tamsayı ${ displaystyle r}$.Natija sifatida, agar ${ displaystyle S}$ bu cheksiz prop koklass guruhi ${ displaystyle r}$, unda minimal tamsayı mavjud emas ${ displaystyle i geq 1}$ shunday qilib har qanday butun son uchun quyidagi uchta shart bajariladi ${ displaystyle j geq i}$.

S

1. ${ displaystyle mathrm {cc} (S / gamma _ {j} (S)) = r}$,
2. ${ displaystyle S / gamma _ {j} (S)}$ har qanday cheksiz pro-ning pastki markaziy qismi emasp koklass guruhi ${ displaystyle r}$ izomorf bo'lmagan narsa ${ displaystyle S}$,
3. ${ displaystyle gamma _ {j} / gamma _ {j + 1} (S)}$ tartibli tsiklikdir ${ displaystyle p}$.

Avlod daraxti ${ displaystyle { mathcal {T}} (R)}$, ildizning ota-ona ta'rifiga (P2) nisbatan ${ displaystyle R = S / gamma _ {i} (S)}$ minimal bilan ${ displaystyle i}$ deyiladi koklass daraxti ${ displaystyle { mathcal {T}} (S)}$ ning ${ displaystyle S}$va uning noyob maksimal cheksiz (teskari yo'naltirilgan) yo'li

${ displaystyle (5) qquad R = S / gamma _ {i} (S) chap tomondagi S / gamma _ {i + 1} (S) chap tomondagi S / gamma _ {i + 2} (S) } leftarrow cdots}$

deyiladi asosiy yo'nalish (yoki magistral) daraxtning.

1-rasm: Avlod daraxt. B (2), B (4) shoxlari 0 chuqurlikka ega va B (5), B (7), resp. B (6), B (8), daraxtlar kabi izomorfdir.

Daraxt diagrammasi

Daraxtlarning cheklangan qismlarini vizualizatsiya qilish diagrammalarida qo'llaniladigan qo'shimcha atamalar 1-rasmda sun'iy mavhum daraxt yordamida tushuntirilgan. Daraja nasldan naslga o'tadigan daraxtning asosiy yuqoridan pastga qarab tuzilishini bildiradi, masalan, 2-rasmdagi beton daraxtlar uchun, resp. 3-rasm va hk., Daraja odatda a bilan almashtiriladi buyurtmalar ko'lami tepadan pastga qarab o'sib boradi.A vertex is qobiliyatli (yoki kengaytiriladigan) agar u kamida bitta zurriyodga ega bo'lsa, aks holda shunday bo'ladi Terminal (yoki a bargUmumiy ota-onani ulashadigan sertifikatlar deyiladi birodarlar.

Agar avlod daraxti koklass daraxti bo'lsa ${ displaystyle { mathcal {T}} (R)}$ ildiz bilan ${ displaystyle R = R_ {0}}$va magistral chiziqlar bilan ${ displaystyle (R_ {n}) _ {n geq 0}}$ darajasiga qarab etiketlanadi ${ displaystyle n}$, keyin farqlar to'plami sifatida aniqlangan cheklangan kichik daraxt

${ displaystyle (6) qquad { mathcal {B}} (n) = { mathcal {T}} (R_ {n}) setminus { mathcal {T}} (R_ {n + 1})}$

deyiladi nfilial (yoki novda) daraxtning yoki shuningdek filial ${ displaystyle { mathcal {B}} (R_ {n})}$ ildiz bilan ${ displaystyle R_ {n}}$, har qanday kishi uchun ${ displaystyle n geq 0}$.The chuqurlik filialning uchlari - bu uning tepalarini ildiz bilan bog'laydigan yo'llarning maksimal uzunligi, 1-rasmda shoxlari bo'lgan sun'iy mavhum koklass daraxti ko'rsatilgan. ${ displaystyle { mathcal {B}} (2)}$ va ${ displaystyle { mathcal {B}} (4)}$ ikkalasi ham chuqurlikka ega ${ displaystyle 0}$va filiallar ${ displaystyle { mathcal {B}} (5) simeq { mathcal {B}} (7)}$ va ${ displaystyle { mathcal {B}} (6) simeq { mathcal {B}} (8)}$ Agar grafikalar kabi juftlik izomorfikdir, agar chuqurlikning barcha tepalari berilgan butun sondan kattaroq bo'lsa ${ displaystyle k geq 0}$ filialdan olib tashlanadi ${ displaystyle { mathcal {B}} (n)}$keyin chuqurlikni olamiz${ displaystyle k}$ kesilgan filial ${ displaystyle { mathcal {B}} _ {k} (n)}$.Shunga mos ravishda, chuqurlik -${ displaystyle k}$ kesilgan koklass daraxti ${ displaystyle { mathcal {T}} _ {k} (R)}$, resp. butun koklass daraxti ${ displaystyle { mathcal {T}} (R)}$, uning kesilgan novdalarining cheksiz ketma-ketligidan iborat ${ displaystyle ({ mathcal {B}} _ {k} (n)) _ {n geq 0}}$, resp. filiallar ${ displaystyle ({ mathcal {B}} (n)) _ {n geq 0}}$, vertikallari magistral chiziq bilan bog'langan ${ displaystyle R_ {n}}$ deyiladi cheksiz qobiliyatli.

Virtual davriylik

Chuqurlik bilan kesilgan koklas xazinalari tarmoqlarining davriyligi isbotlangan analitik usullar zeta funktsiyalaridan foydalanish^[3]M. du Sautoy guruhlari,^[7]va bilan algebraik usullar foydalanish kohomologiya guruhlari B. Eik va C. R. Lidem-Grin tomonidan.^[8]Ilgari usullar sifat tushunchasini tan oladi yakuniy virtual davriylik, oxirgi texnikalar miqdoriy tuzilishini aniqlaydi.

Teorema.Har qanday cheksiz pro- uchunp guruh ${ displaystyle S}$ koklass ${ displaystyle r geq 1}$ va o'lchov ${ displaystyle d}$va har qanday chuqurlik uchun ${ displaystyle k geq 1}$, samarali minimal pastki chegara mavjud ${ displaystyle f (k) geq 1}$, qayerda uzunlikning davriyligi ${ displaystyle d}$ koklass daraxtining kesilgan novdalaridan ${ displaystyle { mathcal {T}} (S)}$ o'rnatadi, ya'ni grafik izomorfizmlari mavjud

${ displaystyle (7) qquad { mathcal {B}} _ {k} (n + d) simeq { mathcal {B}} _ {k} (n)}$ Barcha uchun ${ displaystyle n geq f (k)}$.

Isbot uchun bosing ko'rsatish o'ng tomonda.

Ushbu markaziy natijalarni hayratga soladigan tarzda ifodalash mumkin: biz koklass daraxtiga juft shlaklar orqali qaraganimizda va yuqori qismida davriygacha bo'lgan sonli sonli shoxlarni e'tiborsiz qoldirganimizda, biz takrorlanadigan cheklangan naqshni ko'rayapmiz (yakuniy Ammo, agar biz yanada kengroq miltillovchilarni olsak, davriygacha boshlang'ich bo'lim uzoqroq bo'lishi mumkin (virtual davriylik).

Tepalik ${ displaystyle P = R_ {f (k)}}$ deyiladi davriy ildiz kesilgan koklass daraxtining chuqurligi uchun belgilangan qiymat uchun ${ displaystyle k}$.1-rasmga qarang.

Multifurkatsiya va koklass grafikalari

Faraz qiling, cheklangan ota-onalar p- guruhlar oxirgi ahamiyatsiz pastki markaziy kvotentsiyalar (P2) sifatida aniqlanadi p-grup ${ displaystyle G}$ koklass ${ displaystyle mathrm {cc} (G) = r}$, biz uning (butun) avlod daraxtini ajrata olamiz ${ displaystyle { mathcal {T}} (G)}$va uning koklass-${ displaystyle r}$ avlod daraxti ${ displaystyle { mathcal {T}} ^ {r} (G)}$, bu koklass avlodidan iborat bo'lgan kichik daraxt ${ displaystyle r}$ Faqat guruh ${ displaystyle G}$ deyiladi koklassga joylashtirilgan agar ${ displaystyle { mathcal {T}} (G) = { mathcal {T}} ^ {r} (G)}$, ya'ni avlodlari bo'lmasa ${ displaystyle G}$ dan kattaroq koklass bilan ${ displaystyle r}$.

The yadro darajasi ${ displaystyle nu (G)}$ ning ${ displaystyle G}$nazariyasida p-gruplar yaratish algoritmi M. F. Nyuman tomonidan^[11]va E. A. O'Brayen^[12]quyidagi mezonlarni taqdim etadi.

N

1. ${ displaystyle G}$ terminali hisoblanadi, va shuning uchun ahamiyatsiz koklass bilan o'rnatiladi, agar kerak bo'lsa ${ displaystyle nu (G) = 0}$.
2. Agar ${ displaystyle nu (G) = 1}$, keyin ${ displaystyle G}$ qobiliyatli, ammo noma'lum bo'lib qolmoqda ${ displaystyle G}$ koklass bilan joylashtirilgan.
3. Agar ${ displaystyle nu (G) = m geq 2}$, keyin ${ displaystyle G}$ qobiliyatli va, albatta, koklassga joylashtirilmagan.

Oxirgi holatda aniqroq tasdiqlash mumkin: Agar ${ displaystyle G}$ koklassga ega ${ displaystyle r}$ va yadro darajasi ${ displaystyle nu (G) = m geq 2}$, keyin u toanni keltirib chiqaradi m- multifurkatsiyaichiga muntazam koklass-r avlod daraxt ${ displaystyle { mathcal {T}} ^ {r} (G)}$va ${ displaystyle m-1}$ tartibsiz avlod grafikalar ${ displaystyle { mathcal {T}} ^ {r + j} (G)}$ koklass ${ displaystyle r + j}$,uchun ${ displaystyle 1 leq j leq m-1}$.Bundan kelib chiqqan holda, ${ displaystyle G}$ ajralgan birlashma

${ displaystyle (8) qquad { mathcal {T}} (G) = { dot { cup}} _ {j = 0} ^ {m-1} , { mathcal {T}} ^ { r + j} (G)}$.

Multifurkatsiya yaqin avlodlarning so'nggi ahamiyatsiz pastki markazining turli xil buyruqlari bilan o'zaro bog'liqdir, chunki nilpotensiya sinfi bir birlik tomonidan ko'payadi, ${ displaystyle c = mathrm {cl} (Q) = mathrm {cl} (P) +1}$, ota-onadan ${ displaystyle P = Q / gamma _ {c} (Q) = pi (Q)}$ har qanday bevosita avlodga ${ displaystyle Q}$, koklass barqaror bo'lib qoladi, ${ displaystyle r = mathrm {cc} (Q) = mathrm {cc} (P)}$, agar oxirgi ahamiyatsiz bo'lmagan pastki markaz tartibli tsiklik bo'lsa ${ displaystyle vert gamma _ {c} (Q) vert = p}$, o'shandan beri buyurtma ko'rsatkichi ham birlikka to'liq oshadi, ${ displaystyle vert Q vert = p cdot vert P vert}$ .Ushbu holatda, ${ displaystyle Q}$ a muntazam darhol avlod yo'naltirilgan chekka bilan ${ displaystyle P leftarrow Q}$ ning qadam hajmi ${ displaystyle 1}$, odatdagidek Biroq, koklass ortadi ${ displaystyle m-1}$, agar ${ displaystyle vert gamma _ {c} (Q) vert = p ^ {m}}$ bilan ${ displaystyle m geq 2}$.Shunda ${ displaystyle Q}$ deyiladi tartibsiz darhol avlod yo'naltirilgan chekka bilan ${ displaystyle P leftarrow Q}$ ning qadam hajmi ${ displaystyle m}$.

Agar sharti qadam hajmi ${ displaystyle 1}$ barcha yo'naltirilgan qirralarga, so'ngra maksimal avlod daraxtiga o'rnatiladi ${ displaystyle { mathcal {T}} (1)}$ ahamiyatsiz guruh ${ displaystyle 1}$nihoyatda cheksiz bo'linmagan birlashishga bo'linadi

${ displaystyle (9) qquad { mathcal {T}} (1) = { dot { cup}} _ {r = 0} ^ { infty} , { mathcal {G}} (p, r)}$

yo'naltirilgan koklass grafikalari ${ displaystyle { mathcal {G}} (p, r)}$, aksincha o'rmonlar daraxtlarga qaraganda.To'g'ri, yuqorida aytib o'tilgan Coclass teoremalari shuni nazarda tutadi

${ displaystyle (10) qquad { mathcal {G}} (p, r) = left ({ dot { cup}} _ {i} , { mathcal {T}} (S_ {i}) ) o'ng) { nuqta { cup}} { mathcal {G}} _ {0} (p, r)}$

ning ajralgan birlashmasijuda ko'p koklass daraxtlari ${ displaystyle { mathcal {T}} (S_ {i})}$ izomorf bo'lmagan cheksiz prop guruhlar ${ displaystyle S_ {i}}$ koklass ${ displaystyle r}$ (D teoremasi) va a cheklangan subgraf ${ displaystyle { mathcal {G}} _ {0} (p, r)}$ ning sporadik guruhlar har qanday koklass daraxtining tashqarisida yotish.

Identifikatorlar

The SmallGroups Kutubxona identifikatorlar cheklangan guruhlar, xususan cheklanganlar pshaklida berilgan guruhlar

${ displaystyle langle { text {order}}, { text {hisoblash raqami}} rangle}$

nasl daraxtlarining quyidagi aniq misollarida, H. U.Beshche, B. Eik va E. A. O'Brayenga tegishli.^[13][14]Guruh buyruqlari chap tomonda, 2-rasm va 3-rasmda bo'lgani kabi, shkalada berilganida, identifikatorlar qisqacha bilan belgilanadi

${ displaystyle langle { text {counting number}} rangle}$.

Boshlang'ichga bog'liq ${ displaystyle p}$, SmallGroup identifikatori mavjud bo'lgan guruhlar tartibida yuqori chegara mavjud, masalan. ${ displaystyle 512 = 2 ^ {9}}$ uchun ${ displaystyle p = 2}$va ${ displaystyle 2187 = 3 ^ {7}}$ uchun ${ displaystyle p = 3}$.Kattaroq buyurtmalar guruhlari uchun umumlashtirilgan identifikatorlar nasl-nasab tuzilishiga o'xshaydi, qadam kattaligi chekkasi bilan bog'langan muntazam zudlik bilan avlod ${ displaystyle 1}$ ota-onasi bilan ${ displaystyle P}$, bilan belgilanadi

${ displaystyle P - # 1; { text {hisoblash raqami}}}$,

va qadam kattaligi chekkasi bilan bog'langan tartibsiz darhol avlod ${ displaystyle s geq 2}$ ota-onasi bilan ${ displaystyle P}$, bilan belgilanadi

${ displaystyle P - # s; { text {hisoblash raqami}}}$.

Ning amalga oshirilishi p-gruplar yaratish algoritmi hisoblash algebra tizimlarida GAP va Magma 1979 yilda J. A. Ascione-ga qaytib kelgan ushbu umumlashtirilgan identifikatorlardan foydalaning.^[15]

Daraxtlarning aniq misollari

Barcha misollarda, asosiy narsa ota-onalarning ta'rifi (P2) odatdagi pastki markaziy ketma-ketlikka mos keladi, pastki ko'rsatkichga nisbatan ota-ona ta'rifi (P3) bilan vaqti-vaqti bilan farqlar -p markaziy seriyalar ko'rsatilgan.

Klass 0

Kokil grafigi

${ displaystyle (11) qquad { mathcal {G}} (p, 0) = { mathcal {G}} _ {0} (p, 0)}$

cheklangan p- koklass guruhlari ${ displaystyle 0}$ hech qanday koklass daraxtini o'z ichiga olmaydi va shuning uchun faqat sporadik guruhlardan iborat, ya'ni ahamiyatsiz guruh ${ displaystyle 1}$ va tsiklik guruh ${ displaystyle C_ {p}}$ tartib ${ displaystyle p}$, bu barg (ammo u pastki ko'rsatkichga nisbatan qodir)p markaziy seriyali) ${ displaystyle p = 2}$ The SmallGroup identifikatori ning ${ displaystyle C_ {p}}$ bu ${ displaystyle langle 2,1 rangle}$,uchun ${ displaystyle p = 3}$ bu ${ displaystyle langle 3,1 rangle}$.

Shakl 2: 1-sinf bilan cheklangan 2-guruhlarning koklass grafigi

1-sinf

Kokil grafigi

${ displaystyle (12) qquad { mathcal {G}} (p, 1) = { mathcal {T}} ^ {1} (R) { dot { cup}} { mathcal {G}} _ {0} (p, 1)}$

cheklangan p- koklass guruhlari ${ displaystyle 1}$, shuningdek, deb nomlangan maksimal sinf, noyoblardan iborat koklass daraxti ${ displaystyle { mathcal {T}} ^ {1} (R)}$ ildiz bilan ${ displaystyle R = C_ {p} marta C_ {p}}$, boshlang'ich abeliya p-grup daraja ${ displaystyle 2}$va bitta izolyatsiya qilingan tepalik(ahamiyatsiz guruhga yo'naltirilganligi sababli, xuddi shu koklass grafasida tegishli ota-onasiz terminali etim ${ displaystyle 1}$ qadam o'lchamiga ega ${ displaystyle 2}$), the tsiklik guruh ${ displaystyle C_ {p ^ {2}}}$ tartib ${ displaystyle p ^ {2}}$ sporadik qismida ${ displaystyle { mathcal {G}} _ {0} (p, 1)}$(ammo, bu guruh pastki ko'rsatkichga nisbatan qodir)p daraxt ${ displaystyle { mathcal {T}} ^ {1} (R) = { mathcal {T}} ^ {1} (S_ {1})}$ noyob koklass treeof hisoblanadi cheksiz prop guruh ${ displaystyle S_ {1}}$ koklass ${ displaystyle 1}$.

Uchun ${ displaystyle p = 2}$, resp. ${ displaystyle p = 3}$, ildizning SmallGroup identifikatori ${ displaystyle R}$ bu ${ displaystyle langle 4,2 rangle}$, resp. ${ displaystyle langle 9,2 rangle}$va filialdan koklass grafasining daraxt diagrammasi ${ displaystyle { mathcal {B}} (2)}$ filialgacha ${ displaystyle { mathcal {B}} (7)}$(ga nisbatan hisoblanadi p-tarmoq ildizi tartibining logaritmasi) 2-rasmda tasvirlangan, resp. Shakl 3, bu erda barcha buyurtmalar guruhlari kamida ${ displaystyle p ^ {3}}$ bor metabelian, bu olingan uzunligi bilan abeliya emas ${ displaystyle 2}$(abel guruhlarini ko'rsatadigan kontur kvadratlaridan farqli o'laroq qora disklar bilan ifodalangan tepalar) .3-rasmda kichikroq qora disklar metabeliya 3-guruhlarini bildiradi, bu erda hatto eng katta kichik guruhlar abeliya emas, bu xususiyat metabeliya 2-guruhlari uchun bo'lmaydi. 2-rasmda, chunki ularning barchasi abeliya indeksining kichik guruhiga ega ${ displaystyle p}$ (odatda to'liq bitta) .Koklass daraxti ${ displaystyle { mathcal {G}} (2,1)}$, resp. ${ displaystyle { mathcal {G}} (3,1)}$, davriy ildizga ega ${ displaystyle langle 8,3 rangle}$ va uzunlikning davriyligi ${ displaystyle 1}$ filialdan boshlab ${ displaystyle { mathcal {B}} (3)}$, resp. davriy ildiz ${ displaystyle langle 81,9 rangle}$ va uzunlikning davriyligi ${ displaystyle 2}$ filial bilan sozlash ${ displaystyle { mathcal {B}} (4)}$.Har ikkala daraxt ham chegaralangan chuqurlik shoxlariga ega ${ displaystyle 1}$, shuning uchun ularning virtual davriyligi aslida a qat'iy davriylik.

Biroq, ning koklass daraxti ${ displaystyle { mathcal {G}} (p, 1)}$ bilan ${ displaystyle p geq 5}$ bor cheksiz chuqurlik tarkibida metabel bo'lmagan guruhlar va koklass daraxti mavjud ${ displaystyle { mathcal {G}} (p, 1)}$ bilan ${ displaystyle p geq 7}$ hatto bor cheksiz kenglik, ya'ni qat'iyatli tartibda avlodlar soni ortib borayotgan tartib bilan cheksiz ko'payadi.^[16]

Yordamida Artin transfertlarining yadrolari va maqsadlari, 2-rasm va 3-rasmdagi diagrammalar qo'shimcha ma'lumot bilan ta'minlanishi va quyidagicha o'zgartirilishi mumkin avlodlashtirilgan daraxtlar.

Aniq misollar ${ displaystyle { mathcal {G}} (2,1)}$ va ${ displaystyle { mathcal {G}} (3,1)}$ koklass grafikasi a berish imkoniyatini beradi parametrlangan politsiklik quvvat-komutator taqdimot^[17]to'liq koklass daraxti uchun ${ displaystyle { mathcal {T}} ^ {1} (R) subset { mathcal {G}} (p, 1)}$, ${ displaystyle p in lbrace 2,3 rbrace}$, qo'rg'oshin qismida nasl daraxtlari kontseptsiyasining foydasi sifatida va butun koklass daraxtining davriyligi natijasida qayd etilgan. Ikkala holatda ham guruh ${ displaystyle G in { mathcal {T}} ^ {1} (R)}$ ikki element tomonidan hosil qilinadi ${ displaystyle x, y}$ammo taqdimotda yuqori kommutatorlar ${ displaystyle s_ {j} = lbrack s_ {j-1}, x rbrack}$, ${ displaystyle 3 leq j leq n-1 = mathrm {cl} (G)}$bilan boshlanadi asosiy kommutator ${ displaystyle s_ {2} = lbrack y, x rbrack}$.Nilpotensiya rasmiy ravishda munosabat bilan ifodalanadi ${ displaystyle s_ {n} = 1}$, guruh tartibda bo'lganda ${ displaystyle vert G vert = p ^ {n}}$.

3-rasm: 1-sinf bilan cheklangan 3-guruhlarning koklass grafigi

Uchun ${ displaystyle p = 2}$, ikkita parametr mavjud ${ displaystyle 0 leq w, z leq 1}$ va kompyuter taqdimoti tomonidan berilgan

(13)${ displaystyle { begin {aligned} G ^ {n} (z, w) = & langle x, y, s_ {2}, ldots, s_ {n-1} mid & x ^ {2} = s_ {n-1} ^ {w}, y ^ {2} = s_ {2} ^ {- 1} s_ {n-1} ^ {z}, lbrack s_ {2}, y rbrack = 1, & s_ {2} = lbrack y, x rbrack, s_ {j} = lbrack s_ {j-1}, x rbrack { text {for}} 3 leq j leq n -1 rangle end {hizalangan}}}$

Maksimal sinfning 2 guruhi, ya'ni koklass ${ displaystyle 1}$, uchta shakl davriy cheksiz ketma-ketliklar,

• The dihedral guruhlar, ${ displaystyle D (2 ^ {n}) = G ^ {n} (0,0)}$, ${ displaystyle n geq 3}$, magistral chiziqni shakllantirish (cheksiz qobiliyatli tepaliklar bilan),
• umumlashtirilgan kvaternion guruhlar, ${ displaystyle Q (2 ^ {n}) = G ^ {n} (0,1)}$, ${ displaystyle n geq 3}$, bularning barchasi terminal tepaliklar,
• The yarim yarim guruhlar, ${ displaystyle S (2 ^ {n}) = G ^ {n} (1,0)}$, ${ displaystyle n geq 4}$, ular ham barglardir.

Uchun ${ displaystyle p = 3}$, uchta parametr mavjud ${ displaystyle 0 leq a leq 1}$ va ${ displaystyle -1 leq w, z leq 1}$ va kompyuter taqdimoti tomonidan berilgan

(14)${ displaystyle { begin {aligned} G_ {a} ^ {n} (z, w) = & langle x, y, s_ {2}, ldots, s_ {n-1} mid & x ^ {3} = s_ {n-1} ^ {w}, y ^ {3} = s_ {2} ^ {- 3} s_ {3} ^ {- 1} s_ {n-1} ^ {z} , lbrack y, s_ {2} rbrack = s_ {n-1} ^ {a}, & s_ {2} = lbrack y, x rbrack, s_ {j} = lbrack s_ {j -1}, x rbrack { text {for}} 3 leq j leq n-1 rangle end {hizalangan}}}$

Parametrli 3-guruh ${ displaystyle a = 0}$ parametrlari bo'lgan abelian maksimal kichik guruhiga ega bo'lish ${ displaystyle a = 1}$ Yo'q, aniqrog'i, mavjud abeliya maksimal kichik guruhi, ikkalasidan tashqari qo'shimcha maxsus guruhlar ${ displaystyle G_ {0} ^ {3} (0,0)}$ va ${ displaystyle G_ {0} ^ {3} (0,1)}$, bu erda to'rtta maksimal kichik guruh ham abeliya hisoblanadi.

Har qanday kattaroq koklasdan farqli o'laroq ${ displaystyle r geq 2}$, koklass grafigi ${ displaystyle { mathcal {G}} (p, 1)}$ faqat o'z ichiga oladi p-gruplar ${ displaystyle G}$ abelianizatsiya bilan ${ displaystyle G / G ^ { prime}}$ turdagi ${ displaystyle (p, p)}$, uning noyob izolyatsiya qilingan tepasi bundan mustasno ${ displaystyle C_ {p ^ {2}}}$.Ish ${ displaystyle p = 2}$ teskari bayonotning haqiqati bilan ajralib turadi: Turli abelianizatsiya bilan har qanday 2-guruh ${ displaystyle (2,2)}$ koklassdan iborat ${ displaystyle 1}$ (O. Tausskiy teoremasi.)^[18]).

Shakl 4: (3,3) turdagi 1 va 2-sonli koklasning cheklangan 3-guruhlari o'rtasidagi interfeys

2-sinf

Koklas grafigining genezisi ${ displaystyle { mathcal {G}} (p, r)}$ bilan ${ displaystyle r geq 2}$ bir xil emas.p- bir nechta aniq abelianizatsiyaga ega bo'lgan guruhlar uning konstitutsiyasiga hissa qo'shadi ${ displaystyle r = 2}$, guruhlarning muhim hissalari mavjud ${ displaystyle G}$ abelianizatsiya bilan ${ displaystyle G / G ^ { prime}}$ turlaridan${ displaystyle (p, p)}$, ${ displaystyle (p ^ {2}, p)}$, ${ displaystyle (p, p, p)}$va tsiklik guruh tomonidan ajratilgan hissa ${ displaystyle C_ {p ^ {3}}}$ tartib ${ displaystyle p ^ {3}}$:

${ displaystyle (15) qquad { mathcal {G}} (p, 2) = { mathcal {G}} _ {(p, p)} (p, 2) { dot { cup}} { mathcal {G}} _ {(p ^ {2}, p)} (p, 2) { dot { cup}} { mathcal {G}} _ {(p, p, p)} (p , 2) { dot { cup}} { mathcal {G}} _ {(p ^ {3})} (p, 2)}$.

Turning abelianizatsiyasi (p,p)

Aksincha p- koklass guruhlari ${ displaystyle 2}$ turdagi abelianizatsiya bilan ${ displaystyle (p ^ {2}, p)}$ yoki ${ displaystyle (p, p, p)}$, ular abeliyaning doimiy avlodlari sifatida paydo bo'ladi p- bir xil turdagi guruhlar,p- koklass guruhlari ${ displaystyle 2}$ turdagi abelianizatsiya bilan ${ displaystyle (p, p)}$abeliyalik bo'lmagan avlodlardan kelib chiqadi p- koklass guruhi ${ displaystyle 1}$ bu koklassga o'rnatilmagan.

Bosh vazir uchun ${ displaystyle p = 2}$, bunday guruhlar umuman mavjud emas, chunki 2-guruh ${ displaystyle langle 8,3 rangle}$ Tausskiy teoremasi uchun chuqurroq sabab bo'lgan koklass joylashtirilgan, bu ajoyib fakt G. Bagnera tomonidan kuzatilgan^[19]allaqachon 1898 yilda.

Toq sonlar uchun ${ displaystyle p geq 3}$, mavjudligi p- koklass guruhlari ${ displaystyle 2}$ turdagi abelianizatsiya bilan ${ displaystyle (p, p)}$guruh ekanligi bilan bog'liq ${ displaystyle G_ {0} ^ {3} (0,0)}$ uning yadro darajasi tengdir ${ displaystyle 2}$, bu esa a ni keltirib chiqaradi ikkiga bo'linish avlod daraxtining ${ displaystyle { mathcal {T}} (G_ {0} ^ {3} (0,0))}$ ikkita koklass grafikasiga ${ displaystyle { mathcal {T}} ^ {1} (G_ {0} ^ {3} (0,0))}$noyob daraxtning kichik daraxtidir ${ displaystyle { mathcal {T}} ^ {1} (C_ {p} marta C_ {p})}$ koklass grafikasida ${ displaystyle { mathcal {G}} (p, 1)}$.To'g'ri bo'lmagan komponent ${ displaystyle { mathcal {T}} ^ {2} (G_ {0} ^ {3} (0,0))}$subgrafga aylanadi ${ displaystyle { mathcal {G}} = { mathcal {G}} _ {(p, p)} (p, 2)}$ koklass grafigi ${ displaystyle { mathcal {G}} (p, 2)}$qadam o'lchamining birlashtiruvchi qirralari bo'lganda ${ displaystyle 2}$ tartibsiz bevosita avlodlarining ${ displaystyle G_ {0} ^ {3} (0,0)}$ olib tashlandi.

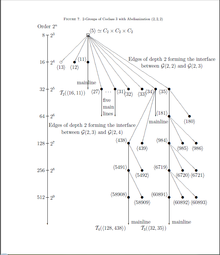
Uchun ${ displaystyle p = 3}$, ushbu subgraf ${ displaystyle { mathcal {G}}}$ 4-rasmda chizilgan bo'lib, unda koklass bilan cheklangan 3-guruhlar o'rtasidagi interfeys ko'rsatilgan ${ displaystyle 1}$ va ${ displaystyle 2}$ turdagi ${ displaystyle (3,3)}$.${ displaystyle { mathcal {G}}}$ uchta muhim turdagi ettita yuqori darajadagi tepaliklarga ega, ularning barchasi buyurtmaga ega ${ displaystyle 243 = 3 ^ {5}}$G. Bagnera tomonidan kashf etilgan.^[19]

• Birinchidan, ikkita terminal mavjud Schur b-guruhlari ${ displaystyle langle 243,5 rangle}$ va ${ displaystyle langle 243,7 rangle}$ sporadik qismida ${ displaystyle { mathcal {G}} _ {0} (3,2)}$ koklass grafigi ${ displaystyle { mathcal {G}} (3,2)}$.
• Ikkinchidan, ikki guruh ${ displaystyle G = langle 243,4 rangle}$ va ${ displaystyle G = langle 243,9 rangle}$ cheklangan daraxtlarning ildizlari ${ displaystyle { mathcal {T}} ^ {2} (G)}$ sporadik qismida ${ displaystyle { mathcal {G}} _ {0} (3,2)}$. Biroq, ular koklassga o'rnatilmaganligi sababli, to'liq daraxtlar ${ displaystyle { mathcal {T}} (G)}$ cheksizdir.
• Nihoyat, uchta guruh ${ displaystyle langle 243,3 rangle}$, ${ displaystyle langle 243,6 rangle}$ va ${ displaystyle langle 243,8 rangle}$ (cheksiz) koklass daraxtlarini tug'dirish, masalan, ${ displaystyle { mathcal {T}} ^ {2} ( langle 729,40 rangle)}$, ${ displaystyle { mathcal {T}} ^ {2} ( langle 243,6 rangle)}$, ${ displaystyle { mathcal {T}} ^ {2} ( langle 243,8 rangle)}$, har biri metabel magistraliga ega, koklass grafasida ${ displaystyle { mathcal {G}} (3,2)}$. Ushbu uchta guruhning birortasi ham koklass bilan o'rnatilmagan.

Artin o'tkazmalari yadrolari va maqsadlari to'g'risida qo'shimcha ma'lumotlarni namoyish qilib, biz ushbu daraxtlarni shunday chizishimiz mumkin avlodlashtirilgan daraxtlar.

Ta'rif.Odatda, a Schur guruhi (a deb nomlangan yopiq kontseptsiyani ishlab chiqqan I. Shur guruhi) pro-p guruh ${ displaystyle G}$ whoserelation martabasi ${ displaystyle d_ {2} (G) = mathrm {dim} _ { mathbb {F} _ {p}} ( mathrm {H} ^ {2} (G, mathbb {F} _ {p} ))}$ uning generator darajasiga to'g'ri keladi ${ displaystyle d_ {1} (G) = mathrm {dim} _ { mathbb {F} _ {p}} ( mathrm {H} ^ {1} (G, mathbb {F} _ {p} ))}$.A b-guruh pro-p guruh ${ displaystyle G}$ bu avtomorfizmga ega ${ displaystyle sigma in mathrm {Aut} (G)}$inversiyani keltirib chiqarish ${ displaystyle x mapsto x ^ {- 1}}$ uning abeliyatsiyasi to'g'risida ${ displaystyle G / G ^ { prime}}$.A Schur b guruhi Schur guruhidir ${ displaystyle G}$ bu ham σ-guruhga kiradi va cheklangan abelizatsiyaga ega ${ displaystyle G / G ^ { prime}}$.

${ displaystyle langle 243,3 rangle}$ koklass daraxtining ildizi emas,

uning bevosita avlodidan beri ${ displaystyle langle 729,40 rangle}$Metabel magistral tepaliklari bo'lgan koklass daraxtining ildizi bo'lgan ikkita aka-uka bor ${ displaystyle langle 729,35 rangle}$, resp. ${ displaystyle langle 729,34 rangle}$, bu bitta, respni keltirib chiqaradi. uchtasi, tsiklik tartib markazlariga ega bo'lgan metabel bo'lmagan magistral tepaliklari bo'lgan koklass daraxti ${ displaystyle 3}$va juda murakkablikdagi shoxlar, ammo shunga qaramay cheklangan chuqurlik ${ displaystyle 5}$.

Jadval 1: G = G (f, g, h) guruhlarining takliflari ^[5]

Parametrlar ${ displaystyle (f, g, h)}$	Abeliyatsiya ${ displaystyle G / G ^ { prime}}$	Sinf-2 ${ displaystyle G / gamma _ {3} (G)}$	3-sinf ${ displaystyle G / gamma _ {4} (G)}$	4-sinf ${ displaystyle G / gamma _ {5} (G)}$
${ displaystyle (0,1,0)}$	${ displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ displaystyle langle 243,3 rangle}$	${ displaystyle langle 729,40 rangle}$
${ displaystyle (0,1,2)}$	${ displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ displaystyle langle 243,6 rangle}$	${ displaystyle langle 729,49 rangle}$
${ displaystyle (1,1,2)}$	${ displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ displaystyle langle 243,8 rangle}$	${ displaystyle langle 729,54 rangle}$
${ displaystyle (1,0,0)}$	${ displaystyle (9,3)}$	${ displaystyle langle 81,3 rangle}$	${ displaystyle langle 243,15 rangle}$	${ displaystyle langle 729,79 rangle}$
${ displaystyle (0,0,1)}$	${ displaystyle (9,3)}$	${ displaystyle langle 81,3 rangle}$	${ displaystyle langle 243,17 rangle}$	${ displaystyle langle 729,84 rangle}$
${ displaystyle (0,0,0)}$	${ displaystyle (3,3,3)}$	${ displaystyle langle 81,12 rangle}$	${ displaystyle langle 243,53 rangle}$	${ displaystyle langle 729,395 rangle}$

Markazi bo'lmagan koklass 2 ning Pro-3 guruhlari

B. Eick, C. R. Lidem-Grin, M. F. Nyuman va E. A. O'Brayen ^[5]koklass bilan cheksiz pro-3 guruhlar oilasini qurdilar ${ displaystyle 2}$ ahamiyatsiz tartib markaziga ega bo'lish ${ displaystyle 3}$.Oila a'zolari uchta parametr bilan tavsiflanadi ${ displaystyle (f, g, h)}$.Ularning cheklangan takliflari barcha velosiped markazlari bilan barcha magistral tepaliklarni hosil qiladi ${ displaystyle (3,3)}$ koklass grafasidagi oltita koklass daraxtining ${ displaystyle { mathcal {G}} (3,2)}$.Parametrlarning ushbu oltita daraxtning ildizlariga bog'lanishi 1-jadvalda, daraxtlarning diagrammalarida keltirilgan, abelyanizatsiya bundan mustasno ${ displaystyle (3,3,3)}$, shakl 4 va shakl 5da ko'rsatilgan va parametrlangan pro-3 taqdimoti quyidagicha berilgan

(16)${ displaystyle { begin {aligned} G (f, g, h) = & langle a, t, z mid & a ^ {3} = z ^ {f}, lbrack t, t ^ { a} rbrack = z ^ {g}, t ^ {1 + a + a ^ {2}} = z ^ {h}, & z ^ {3} = 1, lbrack z, a rbrack = 1, lbrack z, t rbrack = 1 rangle end {hizalangan}}}$

Shakl 5: (9,3) turdagi 2-sonli koklassning 3-guruhlari.

Turning abelianizatsiyasi (p²,p)

Uchun ${ displaystyle p = 3}$, pastki daraxtning yuqori darajalari ${ displaystyle { mathcal {T}} ^ {2} ( langle 27,2 rangle)}$ koklass grafigi ${ displaystyle { mathcal {G}} (3,2)}$ 5-rasmda chizilgan. Ushbu daraxtning eng muhim tepalari umumiy ota-onani baham ko'radigan sakkizta aka-uka ${ displaystyle langle 81,3 rangle}$uchta muhim turdan iborat.

• Birinchidan, uchta barg bor ${ displaystyle langle 243,20 rangle}$, ${ displaystyle langle 243,19 rangle}$, ${ displaystyle langle 243,16 rangle}$ tsiklik tartib markaziga ega ${ displaystyle 9}$va bitta barg ${ displaystyle langle 243,18 rangle}$ turdagi velosiped markazi bilan ${ displaystyle (3,3)}$.
• Ikkinchidan, guruh ${ displaystyle G = langle 243,14 rangle}$ cheklangan daraxtning ildizi ${ displaystyle { mathcal {T}} (G) = { mathcal {T}} ^ {2} (G)}$.
• Nihoyat, uchta guruh ${ displaystyle langle 243,13 rangle}$, ${ displaystyle langle 243,15 rangle}$ va ${ displaystyle langle 243,17 rangle}$ cheksiz koklass daraxtlarini keltirib chiqaradi, masalan. ${ displaystyle { mathcal {T}} ^ {2} ( langle 2187,319 rangle)}$, ${ displaystyle { mathcal {T}} ^ {2} ( langle 243,15 rangle)}$, ${ displaystyle { mathcal {T}} ^ {2} ( langle 243,17 rangle)}$, ularning har biri metabel magistraliga ega, birinchi navbatda tsiklik tartib markazlari mavjud ${ displaystyle 3}$, ikkinchi va uchinchi turdagi velosiped markazlari bilan ${ displaystyle (3,3)}$.

Bu yerda, ${ displaystyle langle 243,13 rangle}$ bu koklass daraxtining ildizi emas, chunki uning avlodidan tashqari ${ displaystyle langle 2187,319 rangle}$metabelian magistral tepaliklari bo'lgan koklass daraxtining ildizi bo'lgan, u beshta avlodga ega bo'lib, ular tsiklik tartib markazlariga ega bo'lgan metabelian bo'lmagan magistral chiziqli koklass daraxtlarini keltirib chiqaradi. ${ displaystyle 3}$va o'ta murakkablik shoxlari, bu erda qisman hatto cheksiz chuqurlik.^[5]

Shakl 6: 2,3,4 va (2,2,2) turdagi koklasning cheklangan 2-guruhlari.

Turning abelianizatsiyasi (p,p,p)

Uchun ${ displaystyle p = 2}$, resp. ${ displaystyle p = 3}$bilan noyob koklass daraxti mavjud p- turdagi guruhlar ${ displaystyle (p, p, p)}$ koklass grafikasida ${ displaystyle { mathcal {G}} (p, 2)}$.Uning ildizi elementar abeliya p- tur guruhi ${ displaystyle (p, p, p)}$, anavi, ${ displaystyle langle 8,5 rangle}$, resp. ${ displaystyle langle 27,5 rangle}$.Bu noyob daraxt oilaning pro-2 guruhiga to'g'ri keladi ${ displaystyle # 59}$ M. F. Nyuman va E. A. O'Brayen tomonidan,^[6]resp. parametrlari bilan berilgan pro-3 guruhiga ${ displaystyle (f, g, h) = (0,0,0)}$ 1-jadvalda ${ displaystyle p = 2}$, daraxt 6-rasmda ko'rsatilgan bo'lib, unda koklass bilan cheklangan 2-guruh ko'rsatilgan ${ displaystyle 2,3,4}$ turdagi ${ displaystyle (2,2,2)}$.

3-sinf

Bu erda yana, p- bir nechta aniq abelianizatsiyaga ega bo'lgan guruhlar koklass grafigi konstitutsiyasiga hissa qo'shadi ${ displaystyle { mathcal {G}} (p, 3)}$.Muntazam ravishda mavjud. guruhlarning tartibsiz, muhim hissalari ${ displaystyle G}$ abelianizatsiya bilan ${ displaystyle G / G ^ { prime}}$ turlaridan${ displaystyle (p ^ {3}, p)}$, ${ displaystyle (p ^ {2}, p ^ {2})}$, ${ displaystyle (p ^ {2}, p, p)}$, ${ displaystyle (p, p, p, p)}$, resp. ${ displaystyle (p, p)}$, ${ displaystyle (p ^ {2}, p)}$, ${ displaystyle (p, p, p)}$va tsiklik guruh tomonidan ajratilgan hissa ${ displaystyle C_ {p ^ {4}}}$ tartib ${ displaystyle p ^ {4}}$.

Turning abelianizatsiyasi (p,p,p)

Boshlang'ich abeliyadan beri p-grup ${ displaystyle C_ {p} times C_ {p} times C_ {p}}$ daraja ${ displaystyle 3}$, anavi,${ displaystyle langle 8,5 rangle}$, resp. ${ displaystyle langle 27,5 rangle}$, uchun ${ displaystyle p = 2}$, resp. ${ displaystyle p = 3}$, koklass bilan o'rnatilmagan, bu ko'p qirrali turtki beradi.Muntazam komponent ${ displaystyle { mathcal {T}} ^ {2} (C_ {p} marta C_ {p} marta C_ {p})}$ koklass haqida bo'limda tasvirlangan ${ displaystyle 2}$.To'g'ri bo'lmagan komponent ${ displaystyle { mathcal {T}} ^ {3} (C_ {p} marta C_ {p} marta C_ {p})}$subgrafga aylanadi ${ displaystyle { mathcal {G}} = { mathcal {G}} _ {(p, p, p)} (p, 3)}$ koklass grafigi ${ displaystyle { mathcal {G}} (p, 3)}$qadam o'lchamining birlashtiruvchi qirralari bo'lganda ${ displaystyle 2}$ tartibsiz bevosita avlodlarining ${ displaystyle C_ {p} times C_ {p} times C_ {p}}$ olib tashlandi.

Uchun ${ displaystyle p = 2}$, ushbu subgraf ${ displaystyle { mathcal {G}}}$ 6-rasmda joylashgan bo'lib, u eng yuqori darajadagi to'qqizta tepalikka ega ${ displaystyle 32 = 2 ^ {5}}$ bu terminal va qobiliyatli tepaliklarga bo'linishi mumkin.

• Ikki guruh ${ displaystyle langle 32,32 rangle}$ va ${ displaystyle langle 32,33 rangle}$ barglar.
• Besh guruh ${ displaystyle langle 32,27..31 rangle}$ va ikki guruh ${ displaystyle langle 32,34..35 rangle}$ cheksiz qobiliyatga ega.

The trees arising from the capable vertices are associated with infinite pro-2 groups by M. F. Newman and E. A. O'Brien^[6]quyidagi tartibda.

${displaystyle langle 32,28 angle }$ gives rise to two trees,

${displaystyle {mathcal {T}}^{3}(langle 64,140 angle )}$ associated with family ${displaystyle #73}$va

${displaystyle {mathcal {T}}^{3}(langle 64,147 angle )}$ associated with family ${displaystyle #74}$.

${displaystyle {mathcal {T}}^{3}(langle 32,29 angle )}$ is associated with family ${displaystyle #75}$.

${displaystyle {mathcal {T}}^{3}(langle 32,30 angle )}$ is associated with family ${displaystyle #76}$.

${displaystyle {mathcal {T}}^{3}(langle 32,31 angle )}$ is associated with family ${displaystyle #77}$.

${displaystyle langle 32,34 angle }$ paydo bo'lishiga olib keladi

${displaystyle {mathcal {T}}^{3}(langle 64,174 angle )}$ associated with family ${displaystyle #78}$. Nihoyat,

${displaystyle {mathcal {T}}^{3}(langle 32,35 angle )}$ is associated with family ${displaystyle #79}$.