To'g'ri morfizm - Proper morphism
Yilda algebraik geometriya, a to'g'ri morfizm o'rtasida sxemalar a-ning analogidir to'g'ri xarita o'rtasida murakkab analitik bo'shliqlar.
Ba'zi mualliflar tegishli deb atashadi xilma-xillik ustidan maydon k a to'liq xilma-xillik. Masalan, har biri proektiv xilma maydon ustida k tugadi k. Sxema X ning cheklangan tip ustidan murakkab sonlar (masalan, xilma-xillik) to'g'ri keladi C agar va faqat bo'sh joy bo'lsa X(C) klassik (evklid) topologiyasi bilan murakkab nuqtalar ixcham va Hausdorff.
A yopiq suvga cho'mish to'g'ri. Morfizm bu cheklangan va agar u to'g'ri bo'lsa va yarim finalli.
Ta'rif
A morfizm f: X → Y sxemalari deyiladi universal yopiq agar har bir sxema uchun Z morfizm bilan Z → Y, dan proektsiya tola mahsuloti
a yopiq xarita asosidagi topologik bo'shliqlar. Sxemalarning morfizmi deyiladi to'g'ri agar shunday bo'lsa ajratilgan, ning cheklangan tip va universal yopiq ([EGA] II, 5.4.1.) [1] ). Bittasi ham shunday deydi X tugadi Y. Xususan, turli xil X maydon ustida k to'g'ri deb aytilgan k agar morfizm X → Spec (k) to'g'ri.
Misollar
Har qanday tabiiy son uchun n, proektsion maydon Pn ustidan komutativ uzuk R tugadi R. Proektsion morfizmlar tegishli, ammo hamma to'g'ri morfizmlar proektiv emas. Masalan, mavjud silliq proektsion bo'lmagan o'lchov 3 ning to'g'ri kompleks xilma-xilligi C.[1] Affin navlari maydon bo'yicha ijobiy o'lchov k hech qachon tugamaydi k. Umuman olganda, to'g'ri afin morfizmi sxemalari cheklangan bo'lishi kerak.[2] Masalan, buni ko'rish qiyin emas afinaviy chiziq A1 maydon ustida k to'g'ri emas k, chunki morfizm A1 → Spec (k) hamma uchun yopiq emas. Darhaqiqat, orqaga tortilgan morfizm
(tomonidan berilgan (x,y) ↦ y) yopiq emas, chunki yopiq ichki to'plamning tasviri xy = 1 dyuym A1 × A1 = A2 bu A1 - yopiq bo'lmagan 0 A1.
Tegishli morfizmlarning xususiyatlari va tavsiflari
Quyidagilarga ruxsat bering f: X → Y sxemalarning morfizmi bo'ling.
- Ikki to'g'ri morfizmning tarkibi to'g'ri keladi.
- Har qanday bazani o'zgartirish to'g'ri morfizm haqida f: X → Y to'g'ri. Ya'ni, agar g: Z → Y bu sxemalarning har qanday morfizmi, keyin hosil bo'lgan morfizmdir X ×Y Z → Z to'g'ri.
- To'g'ri - bu a mahalliy mulk asosida (Zariski topologiyasida). Ya'ni, agar Y ba'zi bir ochiq obzektlar bilan qoplangan Ymen va cheklash f hammaga f−1(Ymen) to'g'ri, keyin ham shunday f.
- Keyinchalik aniqrog'i, muvofiqlik asosda mahalliy hisoblanadi fpqc topologiyasi. Masalan, agar X maydon ustidan sxemadir k va E maydonining kengaytmasi k, keyin X tugadi k agar va faqat taglik o'zgargan bo'lsa XE tugadi E.[3]
- Yopiq suvga cho'mish to'g'ri.
- Umuman olganda, cheklangan morfizmlar to'g'ri keladi. Bu ko'tarilish teorema.
- By Deligne, sxemalar morfizmi, agar u to'g'ri va kvaziyali bo'lsa, cheklangan bo'ladi.[4] Bu ko'rsatgan edi Grothendieck agar morfizm f: X → Y bu cheklangan taqdimotning mahalliy qismida, agar boshqa taxminlardan kelib chiqadigan bo'lsa Y bu noeteriya.[5]
- Uchun X sxema bo'yicha to'g'ri Sva Y ajratilgan S, har qanday morfizmning tasviri X → Y ustida S ning yopiq kichik qismidir Y.[6] Bu topologiyadagi teoremaga o'xshash, ixcham kosmosdan Hausdorff fazosigacha uzluksiz xaritaning tasviri yopiq kichik to'plamdir.
- The Stein faktorizatsiyasi Teoremaning ta'kidlashicha, mahalliy noeteriylar sxemasiga tegishli har qanday to'g'ri morfizm fakt sifatida aniqlanishi mumkin X → Z → Y, qayerda X → Z to'g'ri, sur'ektiv va geometrik bog'langan tolalarga ega va Z → Y cheklangan.[7]
- Chov lemmasi to'g'ri morfizmlar bilan chambarchas bog'liqligini aytadi proektsion morfizmlar. Bitta versiyasi: agar X a dan to'g'ri keladi yarim ixcham sxema Y va X faqat juda ko'p kamaytirilmaydigan tarkibiy qismlarga ega (bu avtomatik ravishda Y noeteriya), keyin proektsion sur'ektiv morfizm mavjud g: V → X shu kabi V proektiv hisoblanadi Y. Bundan tashqari, buni tartibga solish mumkin g zich ochiq pastki qismga nisbatan izomorfizmdir U ning Xva bu g−1(U) zich joylashgan V. Buni ham tartibga solish mumkin V agar ajralmas bo'lsa X ajralmas hisoblanadi.[8]
- Nagata kompaktifikatsiya teoremasi Deligne tomonidan umumlashtirilgandek, kvazi-ixcham va o'rtasida chegaralangan tipdagi morfizm mavjud yarim ajratilgan sxemalar omillari ochiq immersiya, so'ngra to'g'ri morfizm.[9]
- Mahalliy noeteriya sxemalari orasidagi to'g'ri morfizmlar kogerent qatlamlarni saqlaydi, bu ma'noda yuqori to'g'ridan-to'g'ri tasvirlar Rmenf∗(F) (xususan to'g'ridan-to'g'ri tasvir f∗(Fa) ning izchil sheaf F izchil (EGA III, 3.2.1). (Analog ravishda, murakkab analitik bo'shliqlar orasidagi to'g'ri xarita uchun, Grauert va Remmert yuqori to'g'ridan-to'g'ri tasvirlar izchil analitik qirralarni saqlab turishini ko'rsatdi.) Juda alohida holat sifatida: tegishli sxemadagi muntazam funktsiyalarning halqasi X maydon ustida k a kabi cheklangan o'lchovga ega k- vektor maydoni. Aksincha, afine chizig'idagi muntazam funktsiyalarning halqasi tugadi k polinom halqasidir k[x] sifatida cheklangan o'lchovga ega emas k- vektor maydoni.
- Buning biroz kuchliroq bayonoti ham mavjud :(EGA III, 3.2.4) ruxsat bering cheklangan turdagi morfizm bo'lishi, S mahalliy noetherian va a -modul. Agar qo'llab-quvvatlasa F tugadi S, keyin har biri uchun The yuqori to'g'ridan-to'g'ri tasvir izchil.
- Sxema uchun X sonli kompleks sonlar to'plami X(C) murakkab nuqtalar a murakkab analitik makon, klassik (evklid) topologiyadan foydalangan holda. Uchun X va Y ajratilgan va cheklangan turdagi C, morfizm f: X → Y ustida C faqat doimiy xarita bo'lsa, to'g'ri bo'ladi f: X(C) → Y(C) har bir ixcham to'plamning teskari tasviri ixcham ekanligi ma'nosida to'g'ri keladi.[10]
- Agar f: X→Y va g: Y→Z shundaymi? gf to'g'ri va g ajratiladi, keyin f to'g'ri. Buni quyidagi mezon yordamida osonlikcha isbotlash mumkin.
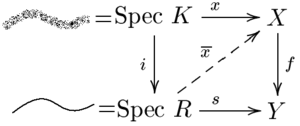
Muvofiqlikning baholash mezoni
Muvofiqlik uchun juda intuitiv mezon mavjud Chevalley. Odatda "." Deb nomlanadi muvofiqlikning baholovchi mezoni. Ruxsat bering f: X → Y sonli tipdagi morfizm bo'lishi noeteriya sxemalari. Keyin f agar hamma uchun bo'lsa va bu to'g'ri bo'lsa diskret baholash uzuklari R bilan kasr maydoni K va har qanday kishi uchun K- baholangan nuqta x ∈ X(K) bir nuqtaga xaritalar f(x) bu aniqlangan R, noyob ko'tarilish mavjud x ga . (EGA II, 7.3.8). Umuman olganda kvazi ajratilgan morfizm f: X → Y sonli turdagi (eslatma: cheklangan turga yarim kompakt kiradi) * har qanday * sxemalar X, Y agar hamma uchun bo'lsa va bu to'g'ri bo'lsa baholash uzuklari R bilan kasr maydoni K va har qanday kishi uchun K- baholangan nuqta x ∈ X(K) bir nuqtaga xaritalar f(x) bu aniqlangan R, noyob ko'tarilish mavjud x ga . (01KF va 01KY teglar to'plami loyihasi). Shuni ta'kidlash kerak Spec K bo'ladi umumiy nuqta ning Spec R va diskret baholash uzuklari aniq muntazam mahalliy bir o'lchovli uzuklar, mezonni qayta o'zgartirish mumkin: muntazam egri berilgan Y (morfizmga mos keladi s: Spec R → Y) va shu egri chiziqning umumiy nuqtasini ko'tarish berilgan X, f egri chiziqni bajarish uchun aniq bitta usul mavjud bo'lsa, mos keladi.
Xuddi shunday, f agar har bir bunday diagrammada ko'pi bilan bitta ko'tarish bo'lsa, ajratiladi .
Masalan, baholash mezonini hisobga olgan holda, ushbu proektsion maydonni tekshirish oson bo'ladi Pn maydonda (yoki hatto tugaganidan keyin) to'g'ri keladi Z). Shaxsiy diskret baholash rishtasi uchun buni shunchaki kuzatish mumkin R kasr maydoni bilan K, har bir K-nuqta [x0,...,xn] proektsion makon an dan kelib chiqadi R-koordinatalarni masshtabini kattalashtirib, hammasi yotadi R va kamida bittasi birlikdir R.
Disklar bilan geometrik talqin
To'g'rilikning baholash mezoniga turtki beradigan misollardan biri bu izohlashdir cheksiz kichik disk sifatida yoki murakkab analitik ravishda disk sifatida . Bu har bir quvvat seriyasidan kelib chiqadi
ba'zi radiusli disklarda birlashadi kelib chiqishi atrofida. Keyinchalik, koordinatalarning o'zgarishini ishlatib, bu birlik diskida quvvat qatori sifatida ifodalanishi mumkin. Keyin, agar biz teskari bo'lsa , bu uzuk kelib chiqishi bilan yo'qolib ketmaydigan kuchlar qatori. Bu topologik jihatdan ochiq disk sifatida namoyish etiladi kelib chiqishi olib tashlangan holda. Sxemalarning morfizmi uchun , bu komutativ diagramma bilan berilgan
Keyinchalik, muvofiqlikni baholash mezonlari fikrni to'ldirish bo'ladi tasvirida .
Misol
Muvofiqlikning baholash mezonlari yopiq ixcham manifoldlarga o'xshash joylarda nima uchun ushlab turilishi kerakligi haqida qarama-qarshi misolni ko'rib chiqish juda yaxshi. Agar olsak va , keyin morfizm ning affine chart orqali omillar , diagrammani kamaytirish
qayerda atrofida joylashgan grafik kuni . Bu komutativ algebralarning komutativ diagrammasini beradi
Keyin, sxemalar diagrammasini ko'tarish, , morfizm mavjudligini anglatadi yuborish algebralarning komutativ diagrammasidan. Bu, albatta, sodir bo'lishi mumkin emas. Shuning uchun to'g'ri emas .
Egri chiziqlar bilan geometrik talqin
Bu teorema nima uchun tutilishi kerakligi haqidagi ba'zi bir sezgi sezgirligini baholash mezonining yana bir shunga o'xshash misoli mavjud. Egri chiziqni ko'rib chiqing va fikrni to'ldiruvchi . Shunda muvofiqlikning baholash mezonlari diagramma sifatida o'qiladi
ko'tarish bilan . Geometrik ravishda bu sxemadagi har bir egri chiziqni anglatadi ixcham egri chiziq bilan yakunlanishi mumkin. Ushbu sezgi biroz topologik bo'shliqlarning morfizmini ixcham tolalar sxemasi-nazariy talqini bilan mos keladi, bu tolalardan biridagi ketma-ketlik birlashishi kerak. Ushbu geometrik vaziyat mahalliy muammo bo'lgani uchun, diagramma mahalliy halqaga qarash bilan almashtiriladi , bu DVR va uning kasr maydoni . Keyin ko'tarish muammosi komutativ diagrammani beradi
bu erda sxema atrofida joylashgan mahalliy diskni aks ettiradi yopiq nuqta bilan olib tashlandi.
Rasmiy sxemalarning to'g'ri morfizmi
Ruxsat bering o'rtasida morfizm bo'lishi mahalliy noetherian rasmiy sxemalari. Biz aytamiz f bu to'g'ri yoki bu to'g'ri ustida agar (i) f bu adik morfizm (ya'ni, ta'rif idealini ta'rif idealiga moslashtiradi) va (ii) induktsiya qilingan xarita to'g'ri, qaerda va K ta'rifining idealidir .(EGA III, 3.4.1) Ta'rif tanlashdan mustaqil K.
Masalan, agar g: Y → Z mahalliy noeteriya sxemalarining to'g'ri morfizmi, Z0 ning yopiq kichik qismidir Zva Y0 ning yopiq kichik qismidir Y shu kabi g(Y0) ⊂ Z0, keyin morfizm rasmiy to'ldirishda rasmiy sxemalarning to'g'ri morfizmi.
Grothendieck ushbu parametrda muvofiqlik teoremasini isbotladi. Ya'ni, ruxsat bering mahalliy noeteriya rasmiy sxemalarining to'g'ri morfizmi bo'ling. Agar F izchil pog'onadir , keyin to'g'ridan-to'g'ri tasvirlar qanchalik baland bo'lsa izchil.[11]
Shuningdek qarang
Adabiyotlar
- ^ Hartshorne (1977), B ilova, 3.4.1-misol.
- ^ Liu (2002), Lemma 3.3.17.
- ^ Stacks Project, 02YJ yorlig'i.
- ^ Grothendieck, EGA IV, 4-qism, Corollaire 18.12.4; Stacks Project, 02LQ yorlig'i.
- ^ Grothendieck, EGA IV, 3 qism, Théorème 8.11.1.
- ^ Stacks Project, 01W0 yorlig'i.
- ^ Stacks Project, 03GX yorlig'i.
- ^ Grothendieck, EGA II, Corollaire 5.6.2.
- ^ Konrad (2007), 4.1-teorema.
- ^ SGA 1, XII taklif 3.2.
- ^ Grothendieck, EGA III, 1 qism, Théorème 3.4.2.
- Konrad, Brayan (2007), "Deligne Nagata kompaktifikatsiyasiga oid yozuvlari" (PDF), Ramanujan Matematik Jamiyati jurnali, 22: 205–257, JANOB 2356346
- Grotendik, Aleksandr; Dieudonne, Jan (1961). "Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques de morfismes". Mathématiques de l'IHÉS nashrlari. 8: 5–222. doi:10.1007 / bf02699291. JANOB 0217084., 5.3-bo'lim. (muvofiqlik ta'rifi), 7.3-bo'lim. (muvofiqlikning baholash mezoni)
- Grotendik, Aleksandr; Dieudonne, Jan (1961). "Eléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Première partie". Mathématiques de l'IHÉS nashrlari. 11: 5–167. doi:10.1007 / bf02684274. JANOB 0217085.
- Grotendik, Aleksandr; Dieudonne, Jan (1966). "Éléments de géométrie algébrique: IV. Étude lokal des schémas et des morfismes de schémas, Troisième partie". Mathématiques de l'IHÉS nashrlari. 28: 5–255. doi:10.1007 / bf02684343. JANOB 0217086., 15.7-bo'lim. (noeteriya sxemalari uchun emas, balki baho mezonlarini umumlashtirish)
- Grotendik, Aleksandr; Dieudonne, Jan (1967). "Éléments de géométrie algébrique: IV. Étude local des des schémas et des morfismes de schémas, Quatrième partie". Mathématiques de l'IHÉS nashrlari. 32: 5–361. doi:10.1007 / bf02732123. JANOB 0238860.
- Xartshorn, Robin (1977), Algebraik geometriya, Berlin, Nyu-York: Springer-Verlag, ISBN 978-0-387-90244-9, JANOB 0463157
- Liu, Tsin (2002), Algebraik geometriya va arifmetik egri chiziqlar, Oksford: Oksford universiteti matbuoti, ISBN 9780191547805, JANOB 1917232
Tashqi havolalar
- V.I. Danilov (2001) [1994], "To'g'ri morfizm", Matematika entsiklopediyasi, EMS Press
- Stacks loyihasi mualliflari, Yig'ma loyihasi









![{ displaystyle { text {Spec}} ( mathbb {C} [[t]])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc33c099b18393b811b4bc4b36b47da7e99dfdf7)




![{ displaystyle mathbb {C} [[t]] [t ^ {- 1}] = mathbb {C} ((t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c613740aad26856289780a3dc2ae2c48ff8d57f3)









![{ displaystyle { begin {matrix} { text {Spec}} ( mathbb {C} ((t))) & to & { text {Spec}} ( mathbb {C} [t, t ^ {-1}]) downarrow && downarrow { text {Spec}} ( mathbb {C} [[t]]) & to & { text {Spec}} ( mathbb {C }) end {matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c90137402723316fe7a1968b3e824759155f5242)
![{ displaystyle { text {Spec}} ( mathbb {C} [t, t ^ {- 1}]) = mathbb {A} ^ {1} - {0 }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9131c02b021a792e30c207d22c47ecb6dc7cac31)

![{ displaystyle { begin {matrix} mathbb {C} ((t)) & leftarrow & mathbb {C} [t, t ^ {- 1}] uparrow && uparrow mathbb { C} [[t]] & leftarrow & mathbb {C} end {matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f76b0e37164b97cc222831de9f43381d60bd05e3)
![{ displaystyle { text {Spec}} ( mathbb {C} [[t]]) to { text {Spec}} ( mathbb {C} [t, t ^ {- 1}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddbfa815e4443f9d485c98ebcbd9666192b259e6)
![{ displaystyle mathbb {C} [t, t ^ {- 1}] to mathbb {C} [[t]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf19229e3d790d3f24abb9b84f0cf192c83d3199)
















